|
structure preserving
“models” of the category Mod. Mazzola is concerned with the contravariant
functor-category
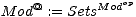 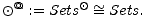  consits of one object . and no arrows besides its identity arrow
(which we identify with .). The evaluation of the corresponding representable functor
@ consits of one object . and no arrows besides its identity arrow
(which we identify with .). The evaluation of the corresponding representable functor
@ 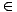 Sets Sets at this one and only object yields .@. = {.} = at this one and only object yields .@. = {.} =  . Recall that Simple . Recall that Simple
 Forms are coordinated by . and have Forms are coordinated by . and have  as their FrameSet. The key to Mazzola’s
ontology is to consider @. as a variable FrameFunctor instead of its only value as their FrameSet. The key to Mazzola’s
ontology is to consider @. as a variable FrameFunctor instead of its only value  and to
replace AmbientSets by their corresponding functors with repect to the isomorpy of
categories Sets and to
replace AmbientSets by their corresponding functors with repect to the isomorpy of
categories Sets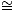 Sets Sets . A new phenomenon in Mazzola’s ontology is the possibility of
Adress variation. Modules play a double role: Each Module A . A new phenomenon in Mazzola’s ontology is the possibility of
Adress variation. Modules play a double role: Each Module A 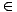 Mod provides a different
viewpoint into a variable “Form”-Functor Fun(F) Mod provides a different
viewpoint into a variable “Form”-Functor Fun(F) 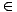 Mod@ and gives access
to a local AmbientSet A@Fun(F) of a Form F. Mazzola calls these functors
FrameSpaces and AmbientSpaces highlighting the geometrical nature of his
approach. Simple Forms are coordinated by Modules M and have the corresponding
representable functors @M as their FrameSpaces. Identifiers are supposed to be
natural functor monomorphsims. Limits, Colimits and Power – constructions are
defined with respect to the functor-category Mod@. The Coordinates of an
A-adressed Denotator of a Form F are defined as an element of the Set A@Fun(F).
The category Mod@ is a Topos, i.e., it has good properties that allow to built
Logics on it. On a metalevel of Metalanguage-Modeling we may consider the
only functor ! : Mod Mod@ and gives access
to a local AmbientSet A@Fun(F) of a Form F. Mazzola calls these functors
FrameSpaces and AmbientSpaces highlighting the geometrical nature of his
approach. Simple Forms are coordinated by Modules M and have the corresponding
representable functors @M as their FrameSpaces. Identifiers are supposed to be
natural functor monomorphsims. Limits, Colimits and Power – constructions are
defined with respect to the functor-category Mod@. The Coordinates of an
A-adressed Denotator of a Form F are defined as an element of the Set A@Fun(F).
The category Mod@ is a Topos, i.e., it has good properties that allow to built
Logics on it. On a metalevel of Metalanguage-Modeling we may consider the
only functor ! : Mod   sending all modules to the pointer .. It induces a
natural transformation !@ : sending all modules to the pointer .. It induces a
natural transformation !@ :  @ @  Mod@ which is an faithfull embedding of
the pointer ontology into Mazzola’s one. AmbientSets in the pointer ontology
correspond to constant AmbientSpaces, i.e., to constant functors in Mazzola’s
ontology. The FrameSet for Simple @ Mod@ which is an faithfull embedding of
the pointer ontology into Mazzola’s one. AmbientSets in the pointer ontology
correspond to constant AmbientSpaces, i.e., to constant functors in Mazzola’s
ontology. The FrameSet for Simple @ -Forms corresponds to the constant functor
sending each module M to -Forms corresponds to the constant functor
sending each module M to  , it is isomorphic to the representable functor of
the Zero Module. Hence all regular, i.e., non-circular, , it is isomorphic to the representable functor of
the Zero Module. Hence all regular, i.e., non-circular,  -Forms correspond to
Forms having only one simple coordinator in their recursive construction: the
Zero-Module. -Forms correspond to
Forms having only one simple coordinator in their recursive construction: the
Zero-Module.
Now recall the
|